Matthew Beckler's Home Page

Home :: Blog :: General :: Software :: Hardware :: Microcontrollers :: Artsy

---

Inkscape: Isometric Projection

From Wikipedia:

Isometric projection is a form of graphical projection — more specifically, an axonometric projection. It is a method of visually representing three-dimensional objects in two dimensions, in which the three coordinate axes appear equally foreshortened and the angles between any two of them is 120°. Isometric projection is one of the projections used in drafting engineering drawings.

In the fields of computer and video games and pixel art, axonometric projection has been popular because of the ease with which 2D sprites and tile-based graphics can be made to represent a 3D gaming environment. Because objects don't change size as they move about the game field, there is no need for the computer to scale sprites or do the calculations necessary to simulate visual perspective. This allowed older 8-bit and 16-bit game systems (and, more recently, handheld systems) to portray large 3D areas easily.

I happen to like drawings done with isometric projection, and recently tried my hand drawing some things at work using Inkscape (download), one of the coolest programs I've used. In one of the drawings, I wanted to add some text that was sitting on a vertical surface, such as the "Welcome" sign in the drawing to the right. I initially tried to simply rotate the text to match the angle, but I soon realized that it wasn't quite right. On the building example, the word "WRONG" was simply rotated, while the word "RIGHT" was skewed, which is the proper operation here.

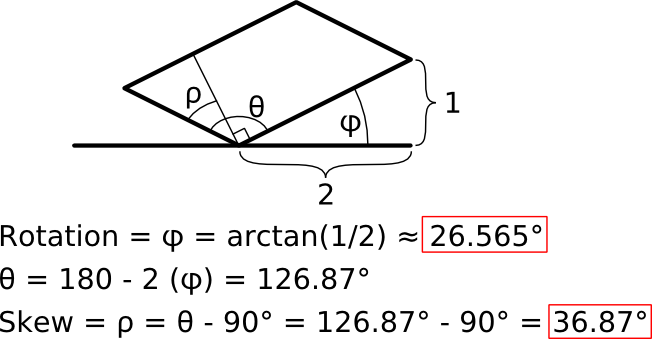
Note: Purists will likely be upset with me, as this isn't strictly isometric projection. For true isometric projection, you need to have all three axes be offset by the same angle, 120°. For computer drawings, we use a 2:1 pixel ratio for the angled lines. This results in an angle of (90° + arctan(1/2)) = 116.565°, which is close enough for our purposes.

You can download my SVG example file that I used to generate the images on this page.

---

Details:

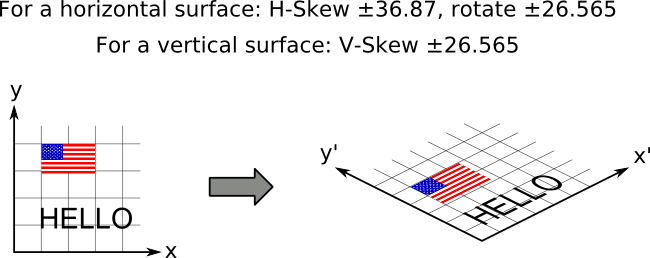
Here, I started with a traditional coordinate system on the left. I redrew the coordinate system in an isometric projection, and transformed the flag and text using the proper transformations.

Place an object on a horizontal surface by first skewing in the horizontal direction by 36.54, and then rotating by 26.565.

Place an object on a vertical surface by simply skewing in the vertical direction by 26.565.

---

Derivation:

---

Copyright © 2004 - 2024, Matthew L. Beckler, CC BY-SA 3.0
Last modified: 2009-09-07 03:04:24 PM (EDT)